Mathematik an der TES

Auf dieser Seite finden Sie die aktuellen Informationen der Fachkonferenz Mathematik zum schulischen Fachcurriculum und zur Unterrichtsgestaltung.

• Stand: November 2025

Für die Planung und Durchführung unseres Unterrichts sind die  Fachanforderungen Mathematik des Landes Schleswig-Holstein die Grundlage.

Zur Vermittlung der fachlichen Kompetenzen greifen wir auf das Lehrwerk “Minimax” des Klett-Verlages zurück. Hier orientieren wir uns auch an dem Stoffverteilungsplan des Lehrwerks. Allerdings kommt es je nach Lernausgangslage und Situation der einzelnen Klassen sowie Schülerinnen und Schüler zu Verschiebungen.

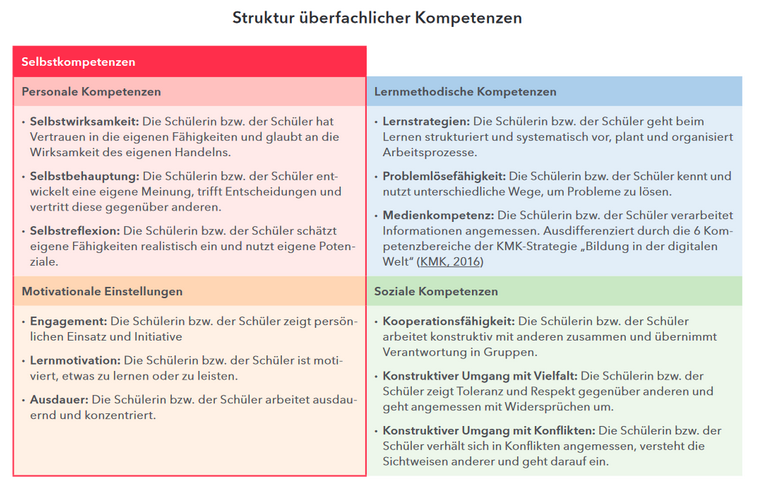
Der Mathematikunterricht besteht nicht nur aus der Vermittlung mathematischer Inhalte. Vielmehr soll auch der Mathematik-Unterricht ganzheitlich wirken und Kompetenzen vermitteln, die weit über das eigentliche Fach Mathematik hinausgehen.

Sprache hat für den Erwerb fachlicher Kompetenzen in Mathematik eine doppelte Funktion: Zum einen dient Sprache als Medium für den Austausch unter Lernenden und die Vermittlung von Wissen.  Der sprachbildende Mathematikunterricht setzt bei der Erkenntnis an, dass sprachliches und fachliches Lernen untrennbar miteinander verbunden sind. Er zielt darauf ab, dass alle Kinder Sprachanregungen erleben und dadurch ihre individuellen sprachlichen und mathematischen Fähigkeiten ausbauen können. Somit wird Sprache im Mathematikunterricht bewusst als Mittel des Kommunizierens und auch des Denkens eingesetzt. Dieses soll bei der Vorbereitung und Durchführung von Unterricht angemessen berücksichtigt werden.

Es geht dabei nicht in erster Linie um die Erarbeitung von Fachausdrücken wie ‚Subtraktion‘ oder ‚Differenz‘. Zentraler ist die (sprachliche) Klärung der mathematischen Konzepte, die hinter diesen Fachausdrücken stecken: ‚Was heißt eigentlich Minusrechnen?‘ bzw. konkret ‚Wie kannst du dir 92 minus 8 vorstellen?‘. Ein sprachbildender Unterricht hat also immer das Verstehen, also den Aufbau von Vorstellungen zum Ziel.

Die Kommunikation über mathematische Konzepte kann dabei nicht nur im Klassenverband oder zwischen Lehrkraft und Kinder stattfinden, sondern auch unter den Kindern (z. B. in Rahmen von Mathekonferenzen).

Für verschiedene Kommunikationsbereiche stehen charakteristische Rede- und Sprechweisen zur Verfügung, die sogenannten sprachlichen Register. In der Schule kommt der „Bildungssprache“ eine zentrale Bedeutung zu, um Kompetenzen und Wissen zu vermitteln, sie wird auch als konzeptionell schriftlich bezeichnet. Sie zeichnet sich durch ausgewählte Sprachhandlungen aus wie Beschreiben, Erklären oder Definieren, durch eher längere Sätze mit komplexeren Strukturen und durch die Verwendung von Fachbegriffen, unpersönlichen Ausdrücken und Nominalisierungen. Weitere für den Mathematikunterricht relevante Register sind die „Alltagssprache“ und die „Fachsprache“.

Für Lehrkräfte ergibt sich die Aufgabe, die individuellen sprachlichen Voraussetzungen und Entwicklungsstände ihrer Lernenden zu diagnostizieren und sie beim sukzessiven Aufbau von sprachlichen Kompetenzen (wie dem Gebrauch von Bildungssprache) zu begleiten. Für die Planung des Mathematikunterrichtes folgt daraus die Notwendigkeit, sprachliche Aktivitäten in den Unterricht zu integrieren, damit Lernende (bildungs-)sprachliche Fähigkeiten erwerben und vertiefen können.

Dazugehörige Materialien finden sich beim Deutschen Zentrum für Lehrkräftebildung Mathematik:

www.pikas.dzlm.de

Heterogenität im Mathematikunterricht

Unterricht hat stets die optimale Förderung aller Schülerinnen und Schüler entsprechend ihrer jeweiligen Begabungen zum Ziel. Daraus ergibt sich, dass Lehr-Lern-Arrangements Maßnahmen beinhalten, die einen differenzierten Zugang zum Unterrichtsgegenstand zum Ziel haben. Die Verschiedenheit von Lernenden ist vielfach beschrieben und lässt sich unter anderem durch die Bereiche Geschlecht, Ethnie, Leistungen im Fach, Alter, spezifische Beeinträchtigungen klassifizieren. 

Um möglichst viele Schülerinnen und Schüler den nächsten Schritt im mathematischen Lernprozess bewältigen zu lassen, bedarf die differenzierende Maßnahme einer möglichst hohen Passung zwischen den Anforderungen der Aufgabe und den individuellen Lernvoraussetzungen. Dazu können bei der Inneren Differenzierung die folgenden Parameter variiert werden:

• Anzahl der zu lösenden Aufgaben (quantitative Differenzierung)
• Qualität der Anforderungen der Aufgaben (qualitative Differenzierung)
• Vorgesehene Bearbeitungszeit (quantitative Differenzierung)
• Hilfemaßnahmen
• Einsatz verschiedener Medien
• Sozialform (soziale Differenzierung)
• Eigenständigkeit bei der Auswahl der Aufgaben (inhaltliche Differenzierung)

An unserer Schule bieten wir zusätzlich additiven Mathematik-Förderunterricht in den Jahrgängen 2-4 an. Hier wird in klassenübergreifenden Lerngruppen noch einmal auf die individuellen Schwierigkeiten von Schülerinnen und Schülern eingegangen.

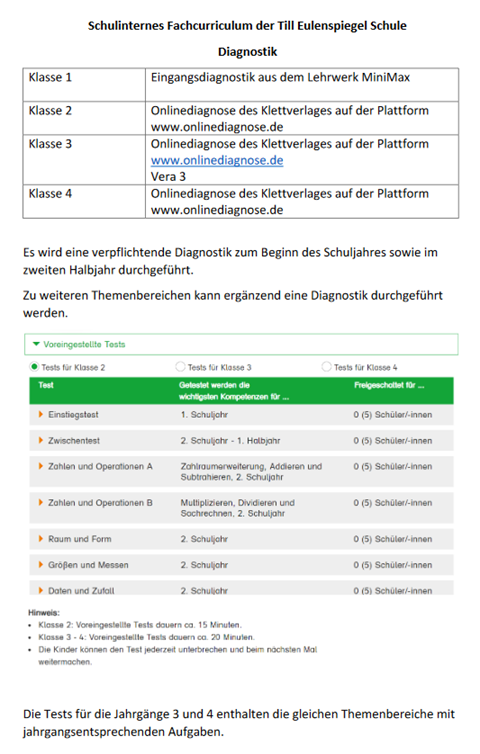
Als Diagnose-Tool nutzen wir die “Online-Diagnose” vom Klett-Verlag:

Als Lehrwerk nutzen wir aktuell das “Minimax” vom Klett-Verlag.

Alle Schülerinnen und Schüler benötigen zusätzlich im Mathematikunterricht vor allem in der Eingangsphase anschauliches, konkretes Material, das angestrebte Kompetenzen begreifbar machen kann. Erst durch konkretes Handeln mit geeignetem Material werden mathematische Grundvorstellungen aufgebaut, die es Kindern ermöglichen, sich allmählich von der konkreten Vorstellung zu lösen und Rechenoperationen ohne Zuhilfenahme von Anschauungsmaterial durchzuführen.

An unserer Schule haben sowohl in der Eingangsphase als auch in den 3. und 4. Klassen Materialkisten, um auch bei den älteren Kindern noch anschaulich Verfahren darstellen zu können und um Kindern ein differenziertes Arbeiten zu ermöglichen.

Hierin befinden sich:

• 20-ger Rechenrahmen
• Steckwürfel
• Bündelungsmaterial für den ZR 1000
• Aufgabenkartei vom Minimax-Lehrwerk

Zusätzlich steht an unserer Schule ein großer Fundus an zusätzlichen Materialien zur Verfügung, welche an einem Materialraum ausgeliehen werden können.

Hierzu gehören u.a.:

• Holzwürfel
• Rechengeld (entsprechend dem Zahlenraum)
• Spielwürfel und ein Spielstein
• Schüttelboxen
• Zahlenstrahl
• 100er Feld mit und ohne Zahlen
• Maßband 1 m
• Lernuhren
• Handspiegel
• Waagen und Gewichtssteine

Der Einsatz digitaler Medien lässt sich aus unterschiedlichen Perspektiven betrachten, und daraus lassen sich jeweils Ableitungen für das unterrichtliche Geschehen vornehmen. Zu nennen sind insbesondere

• der Ansatz der Medienbildung mit seinen übergreifende Kompetenzen im Umgang mit digitalen Medien
• der fachdidaktische Ansatz, bei dem alle verwendeten Technologien das Lernen im Mathematikunterricht in möglichst optimaler Weise unterstützen sollen.

Wir führen ab Jahrgang 1 regelmäßig Medienunterricht an unserer Schule durch. Hier wird der sichere Umgang mit dem iPad gelernt und geübt, die Nutzung von Online-Diagnose-Tools sowie die Nutzung von Lernapps vermittelt. Außerdem lernen die Kinder die Nutzung von “itslearning”, so dass sie selbstständig auf von Lehrkräften online bereitgestelltes Lernmaterial zurückgreifen können.

Als Lernapps nutzen wir aktuell “Anton” und nutzen außerdem die “Mathezeit SH” in Jahrgang 3 und 4.

„Unter basalen mathematischen Kompetenzen werden diejenigen Verstehensgrundlagen gefasst, ohne die ein erfolgreiches, nachhaltig verständiges und weiterführendes Mathematiklernen im Mathematikunterricht nicht möglich ist.“ (SWK, 2022)

Basale Kompetenzen zu fokussieren heißt nicht, nur noch Arithmetik zu unterrichten. Auch andere Inhaltsbereiche und prozessbezogene Kompetenzen (Problemlösen, Kommunizieren/Argumentieren, Darstellen und Modellieren) bleiben unter diesem Fokus wichtig. 

Leseband SH:

Lesen ist eine Kulturtechnik und als grundlegende Kompetenz auch für den Mathematikunterricht unerlässlich. In unserem Leseband SH achten wir darauf, dass dieses auch im Mathematik-Unterricht durchgeführt wird und mathematische Inhalte zum Tragen kommen.

Mögliche Beispiele sind u.a.:

• Rechengeschichten bereits in Klasse 1./2. erlesen und erzählen
• Mathezeit-SH
• Sachaufgaben
• Fermi-Aufgaben
• Recherche

Bewegungsförderung:

Da die Orientierung im Raum eine grundlegende basale Kompetenz ist, die unerlässlich für den gesamten Denkprozess ist, fördern wir die Bewegung im Unterricht an unserer Schule. Für den Mathematik-Unterricht lässt sich dieses mit folgenden Beispielen umsetzen:

• Handlungsorientiertes Arbeiten mit verschiedensten Materialen
• Bewegen auf dem Schulgelände, um Sachsituationen zu entdecken und zu beschreiben
• Bewegen im Klassenraum, um sich passende Materialien selbstständig zu holen

Unserer Leistungsbeurteilung liegen die drei Niveaustufen zugrunde:

• Anforderungsbereich I: Reproduzieren
• Anforderungsbereich II: Zusammenhänge herstellen
• Anforderungsbereich III: Verallgemeinern und Reflektieren 

(Beschluss der Fachkonferenz Mathematik vom 02.04.2019)

• Klasse 3: 100 Multiplikationsaufgaben
• Klasse 4: 100 Aufgaben - 2/3 Multiplikationsaufgaben; 1/3 Divisionsaufgaben

Fehlergrenzen

Das schulinterne Fachcurriculum wird regelmäßig auf den zweimal jährlich durchgeführten Fachkonferenzen überprüft und bei Bedarf abgeändert oder ergänzt und befindet sich deshalb in einem fortlaufenden Prozess. So kann es durchaus auch immer wieder Abweichungen geben, um den Lernausgangslagen und Klassensituationen gerecht zu werden. Es bietet aber eine gute Grundlage und Orientierung, an denen sich die Mitglieder der Schulgemeinschaft halten können.

Unter folgender Adresse sind die aktuellen Fachanforderungen für Schleswig-Holstein abrufbar: